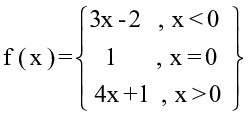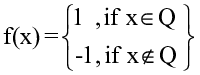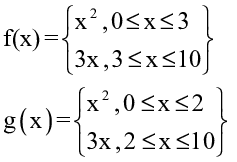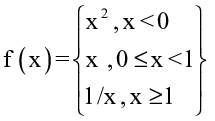Functions
1) Let A = {-2, -1, 0, 1, 2} and if f : A → Z be given by f(x) = x² - 2x - 3. Find the range of f.
- {0, 5, -3, 4}
- {0, -5, -3, -4}
- {0, 5, 3, -4}
- {5, 0, -3, -4}
Answer: {5, 0, -3, -4}
2) Consider the function f (x) = x². Let A = {-2, -1, 0, 1, 2} under this rule f (x) = x² if we obtain f (-2) = 5, f (-1) = 1, f (0) = 0, f (1) = 1 then what could be the functions domain.
- {5, 1, 0, 1}
- None of these
- {-2, -1, 0, 1, 2}
- {3 , 0 , -2 , 2}
Answer: {-2, -1, 0, 1, 2}
3) Let A = {-2, -1, 0, 1, 2} and if f: A → Z be given by f(x) = x² - 2x - 3. Find the pre image of 6
- 7
- 3
- No Pre image
- -6
Answer: No Pre image
4) Find the domain for which the function f(x) = 2x² – 1 and g(x) = 1 - 3x are equal.
- (-2, -1)
- (-2 , -1/2)
- (2, 1/2)
- (-2, 1/2)
Answer: (-2, 1/2)
5) Let f : R → R be a function given by f (x) = x² + 1. Find fˉ¹ (10)
- ±4
- ±5
- No Pre image
- ±3
Answer: ±3
6) Let f = {(1, 1), (2, 3), (0, -1), (-1, -3)} be a function described by the formula f(x) = ax + b. Find a and b.
- (2, 0)
- None of these
- (-2, -1)
- (2, -1)
Answer: (2, -1)
7) Find f (-1) if a function f : R → R be defined by
- 7
- 8
- -5
- 9
Answer: -5
8) If f(x) = x² - 3x + 4, then find the value of f (2x + 1)
- 4x² - 2x - 2
- -4x² - 2x - 2
- 4x
- 4x² - 2x + 2
Answer: 4x² - 2x + 2
9) If f (x) = (x - a)² (x - b)², find f (a + b)
- a²b²
- None of these
- xab
- ab
Answer: a²b²
10) Find the domain for the function f (x) = √(x - 2)
- (-2, ∞]
- (0, 0)
- [2 , ∞)
- [2, -5)
Answer: [2 , ∞)
11) Find the domain for the function f (x) = √(4 - x²)
- [2, -2)
- [2, ∞)
- (- 2, ∞)
- [-2, 2]
Answer: [-2, 2]
12) Find the range of the function f (x) = [(4 - x) / (x - 4 )]
- -1
- x
- 2
- Ø
Answer: -1
13) Find the range of f (x) = [( x - 2) / (3 - x )]
- R → {-1}
- R → {0}
- R → {1}
- R → {2}
Answer: R → {-1}
14) How many terms are there in GP 3, 6, 12, ……., 384?
- 8
- 35
- 30
- 3
Answer: 8
15) Find the 9th term of the GP 2, 4, 8, 16 …….
- 512
- 625
- 320
- 453
Answer: 512
16) Mary buys a Chocolate box A(P) = 50P² - 15p + 30, each Chocolate in the Chocolate box worth p = $3. Find the worth of the Chocolate box.
- 400
- 450
- 345
- 435
Answer: 450
17) Kevin runs in a playground P(t) = 40t² - 30t + 3 meters. The time taken by him, t = 2s. Then find the total distance covered by Kevin.
- 102
- 105
- 100
- 98
Answer: 102
18) In Cadbury city average consumption of Chocolate by a child for respective years are given. Find the rate of change?
- 25
- 14
- 15
- -15
Answer: 15
19) For the function f (x) = (x - 3)². Find the average rate of change between the points at x = 1, x = 3
- -2
- 6
- 3
- 4
Answer: -2
20) Let f be in subset of Z × Z defined by f = {(ab, (a + b) : a, b ∈ Z}. Then f is a
- Composite Function
- Function
- Complement Function
- Not a Function
Answer: Not a Function
21) Find the range of f, if f : R → R be defined as
- [1, 1]
- [0, -1]
- [0, 1]
- [1, -1]
Answer: [1, -1]
22) Determine {x : f(x) = 1}, if f : R → R be such that f (x) = 2 ̽
- 1
- x
- 0
- 4
Answer: 0
23) The function f and g is defined as
- g is a function
- f and g is a function
- f is a function
- f is a function but g is not a function is a function
Answer: f is a function but g is not a function is a function
24) If f (x) = x², find [(f (1.1) - f (1)) / (1.1) - 1]
- 4.1
- 2.1
- 3.1
- 5.1
Answer: 2.1
25) Find the domain of the function f (x) = √(4 - x) + (1 / √(x² - 1))
- (-∞, -1) ∪ ( 1, 4]
- (∞, 1) ∪ (1, 4]
- (-∞, -1) ∪ (-1, -4]
- (∞, -1) ∪ (1, 4]
Answer: (-∞, -1) ∪ ( 1, 4]
26) Find the domain of the function f(x) = (1/2 - sin3x)
- N
- Odd numbers
- R
- Even numbers
Answer: R
27) Find f (-√(3))
- -3
- 4
- 3
- -4
Answer: -4
28) Find the range of the function f(x) = 3 / (2 - x²)
- (-∞, 0) ∪ [1, ∞)
- (-∞, 0) ∪ [ -1 , ∞)
- ( ∞ , 0 ) ∪ [1 , ∞)
- (-∞, 0 ) ∪ [-1, -∞)
Answer: (-∞, 0) ∪ [1, ∞)
29) Find the range of the function f(x) = 3 / (2 - x²)
- (∞, 0) ∪ [3/2, ∞)
- (∞ , 0 ) ∪ [-3/2 , ∞)
- (-∞ , 0 ) ∪ [ 3/2 , ∞)
- (-∞, 0 ) ∪ [-3/2 , -∞)
Answer: (-∞ , 0 ) ∪ [ 3/2 , ∞)
30) Find the general term of the progression 1/4, -1/2, 1, -2
- (-1)ⁿˉ³ (-2)ⁿˉ³
- (-1)ⁿˉ³ (2)ⁿˉ³
- (-1)ⁿˉ⁴ (2)ⁿˉ³
- (-1)ⁿ (2)ⁿˉ³
Answer: (-1)ⁿ (2)ⁿˉ³